الفرق بين المراجعتين لصفحة: «طريقة التنصيف»
ط (١ مراجعة: الصفحات في تصنيف رياضيات) |
(لا فرق)
|
المراجعة الحالية بتاريخ 21:16، 12 نوفمبر 2010
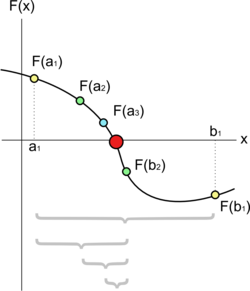
في الرياضيات، تعتبر طريقة التنصيف إحدى طرق خوارزمية إيجاد الجذر والتي بها يتم تنصيف فترة ما بصورة تكرارية و اختيار فترة فرعية يقع عليها الجذر من أجل تحسين المعالجة. مع أنها بسيطة جدا ومرنة إلا أن طريقة التنصيف بطيئة نسبيا.
الطريقة
يمكن تطبيق الطريقة عند الحاجة لحل المعادلة لمتغير المتجه القياسي x, حيث f دالة متصلة.
التحليل
كود برمجي
فيما يلي كود بلغة فجول بيسك يوضح طريقة التنصيف. المتغيرات left وright تقابل a and b أعلاه. القيم الأولية left وright ينبغي اختيارها بالشكل الصحيح بحيث f(left) وf(right) بحيث تكون ذات إشارات مخالفة (لحصر الجذر). المتغير epsilon يبين مدى الدقة المطلوبة.
'Bisection Method
'Start loop
Do While (abs(right - left) > 2*epsilon)
'Calculate midpoint of domain
midpoint = (right + left) / 2
'Find f(midpoint)
If ((f(left) * f(midpoint)) > 0) Then
'Throw away left half
left = midpoint
Else
'Throw away right half
right = midpoint
End If
Loop
Return (right + left) / 2
اعتبارات تطبيقية
إنظر أيضا
المصادر
- Burden, Richard L.; Faires, J. Douglas (2000), Numerical Analysis (7th ed.), Brooks/Cole, ISBN 978-0-534-38216-2.
- Corliss, George (1977), "Which root does the bisection algorithm find?", SIAM Review 19 (2): 325–327, doi:10.1137/1019044, ISSN 1095-7200.
- Kaw, Autar; Kalu, Egwu (2008), Numerical Methods with Applications (1st ed.). http://numericalmethods.eng.usf.edu/topics/textbook_index.html
cs:Půlení intervalů de:Bisektion en:Bisection method es:Método de bisección fr:Méthode de dichotomie he:שיטת החצייה id:Metode bagi-dua it:Metodo della bisezione ja:二分法 ko:이분법 (수학) nl:Bisectie pl:Metoda równego podziału ru:Метод бисекции sl:Bisekcija (numerična metoda) sr:Метода половљења интервала sv:Bisektionsmetoden zh:二分法