الفرق بين المراجعتين لصفحة: «متوازي أضلاع القوى»
ط (مراجعة واحدة) |
(لا فرق)
|
المراجعة الحالية بتاريخ 19:36، 11 سبتمبر 2013
متوازي أضلاع القوى (بالإنجليزية: Parallelogram of force ) هو متوازي اضلاع يتبع أحد قوانين الميكانيكا والذي ينص على أن:" إذا عملت قوتان في نقطة فيمكن أن يعبر عنهما بقوة واحدة." تسمى تلك القوة "محصلة". عمليا نقوم برسم متجهين للقوتين (أي نختار طول معين لكل منهما ) ونمثل اتجاهيهما بسهمين . نرسم متوازيان للسهمين فيكمل تقاطعهما شكل متوازي الأضلاع. المحور الواصل ينقكة تأثير القوتان والنقطة المقابلة على متوازي الأضلاع هي محصلة القوتين ، واتجاه المحصل يكون بادئا مننقطة تاثير القوتين .
معكوس تلك العملية يسمى تحليل قوة ، حيث نجزيء متجها للقوى إلى مركبتين عموديتان على بعضهما البعض ، فإذا عرفنا اتجاه تأثير المركبتين نستطيع تعيين مقدار كل منهما .
يمكن تعمميم هذه الطريقة للحصول على محصلة عدة قوي ، ثلاثة أو أربعة أو أكثر... فيما يسمى زوايا القوى .
جمع قوتان بالرسم البياني
نفترض أن قوتين تؤثر على جسم في نقطة معينة. يمكننا بواسطة الرسم البياني تعيين المحصلة ، كالآتي:
- نرسم القوتان كسهمين بمقياس رسم معين ، من حيث المقدار والاتجاه ،
- نرسم من رأس السهم الأول خطا موازيا للسهم الثاني ،
- ونرسم من رأس السهم الثاني خطا موازيا للسهم الأول . يتقاع الخطان ويكتمل متوازي الأضلاع .
- المحور الباديء من نقطة تأثير القوتين إلى نقطة تقاطع الخطين هي محصلة القوتين ، وتقوم مقامهما .
تعيين محصلة قوتين
وإذا عملت قوتان مختلفتان و في اتجاهين متضادين تكون محصلتهما مساوية لحاصل طرح القوة الصغيرة من القوة الكبيرة. وتكون القوة الناتجة في اتجاه القوة الكبيرة ومقدارها هو القيمة المطلقة لحاصل الطرح :
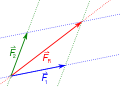
وإذا عملت قوتان مختلفتي الاتجاه على نقطة نحصل على قيمة واتجاه محصلتهما عن طريق رسم متوازي أضلاع القوى لهما . نرسم القوة و القوة بمقياس رسم ثابت بحيث يعبر طول السهم الأول عن القوة الأولى واتجاهها. ومن نقطة تأثيرهما نرسم سهما ثانيا مساويا في الطول لقيمة القوة مع أخذ الزاوية بينهما في الاعتبار . ثم نرسم موازيا من طرف السهم الأول موازيا للقوة الثانية ، ونرسم من طرف القوة الثانية موازيا للقوة الأولى . بذلك نحصل على متوازي أضلاع القوي ، وفيه يمثل المحور الواصل بين نقطة تأثير القوتين والنقطة المقابلة لها على متوازي أضلاع القوي هو محصلة القوة . طول المحور هو مقدار المحصلة ( بحسب مقياس الرسم) وأتجاه المحور يعطينا اتجاة المحصلة .
وإذا عملت ثلاثة قوى في نقطة فيمكن تعيين محصلتهم بسهولة : نرسم متوازي أضلاع القوي لأي اثنين من القوى أولا ونحصل على محصلتهما . ثم نرسم المحصلة التي حصلنا عليها للقوتين الأولتين مع سهم القوة الثالثة ، فنحصل على محصلة الثلاثة قوى .
تحليل قوة
نفترض جسما موضوعا على لوح . تعمل قوة الجاذبية للجسم إلى أسفل وتتساوى معها القوة المضادة للوح الموضوع أفقيا فيظل الجسم ثابتا. أما إذا كان اللوح مائلا فيمكننا دراسة القوى المؤثرة على الجسم (انظر الشكل) . قوة الجاذبية للكتلة تعمل راسيا . ويمكن تحليل هذه القوة إلى جزئين : مركّبة في اتجاه العمودي على السطح F2 ، ومركبة F1 في اتجاه موازي للسطح المائل . إذا زادت القوة F1 عن قوة الاحتكاك بين الجسم والسطح ينزلق الجسم متسارعا على السطح ويسقط . من الواضح ان هذا يعتمد على زاوية ميل ألفا السطح الموضوع عليه الجسم .
وتنطبق المعادلة الناتجة عن تحليل القوة ::
بمثل هذه التجربة يمكن تعيين قوة احتكاك الجسم باللوح ودراسة التسارع .