الفرق بين المراجعتين لصفحة: «توزيع بواسون»
ط (١ مراجعة: الصفحات في تصنيف رياضيات) |
(لا فرق)
|
مراجعة 21:15، 12 نوفمبر 2010
دالة الكثافة الاحتمالية 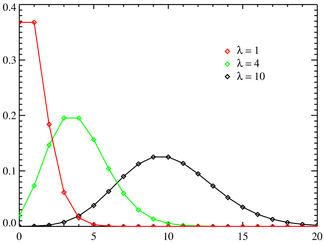 | |
دالة التوزيع التراكمي 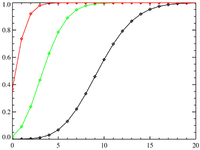 | |
| المؤشرات | |
| الدعم | |
| قالب:توزيع احتمالي/رابط كثافة | |
| د۔ت۔ت | |
| المتوسط الحسابي | |
| الوسيط الحسابي | |
| المنوال | |
| التباين | |
| التجانف | |
| التفرطح | |
| الاعتلاج | |
| د۔م۔ع | |
| الدالة المميزة | |
| معلومات فيشر | {{{معلومات فيشر}}} |
في علمي الإحصاء والاحتمالات، توزيع بواسون (بالإنجليزية: Poisson distribution) (ويسمى أيضا قانون بواسون للأعداد الصغيرة[1]) هو توزيع احتمالي منفصل (en) يعبر عن احتمالية حدوث عدد من الأحداث ضمن فترة محددة من الوقت إذا حدثت هذه الأحداث بمعدل وسطي معروف وغير متعلقة بزمن حدوث آخر حدث.
في مدّة زمنية T، يحصل الحدث بمعدل λ مرّات (λ أقل من 5 مثلا). لنرمز بX المتغير العشوائي الذي يمثل عدد المرّات التي سيحصل فيها الحدث في X. T يمكن أن يساوي 0، 1، 2...
يتبع هذا المتغير العشوائي القانون التالي:
مهما كان العدد الطبيعي k.
- λعدد حقيقي موجب
- (p(k : احتمال حصول الحدث k في T.
هذا ما يدعى توزيع بواسون (أو قانون بواسون) ذا المعلمة λ.
حساب (p(k
يقام حساب هذه الكمية نتيجة عن العمل بتوزيع ثنائي ذا المعلمتين (T ; λ/T). إذا اعتبرنا T كبيرا، فيمكن تبيين أن التوزيع الثنائي نهايته في اللانهاية هو توزيع بواسون.
القيمة المتوقعة، التباين والانحراف المعياري
- القيمة المتوقعة لتوزيع بواسون هي λ
- تباين توزيع بواسون λ
- الانحراف المعياري لتوزيع بواسون هو
ميادين الاستعمال
غالبا ما استعمل توزيع بواسون لحساب أحداث النادرة كانتحار الأطفال، وصول البواخر إلى المرسى أو الحوادث الناتجة عن ركالات الأحصنة في العساكر (دراسة لاديسلاوس بورتكيفيكز)
أما منذ بعض عشرات السنين، امتد استعمال توزيع بواسون إلى ميادين أخرى. فهو يستعمل كثيرا الآن في تكنولوجيات الإتصال (حساب عدد المواصلات في مدّة معينة)، مراقبة الجودة الإحصائية، وصف بعض الظواهر التابعة لميدان التفكيك النووي المشع (تفكيك النواة المشعة يتبع دالة أسية ذات معملة تدعى أيضا λ) وعلم الأحياء والرصد الجوي...
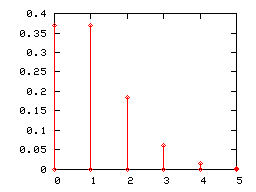
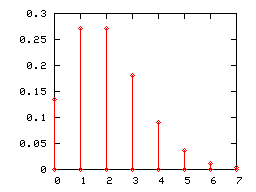
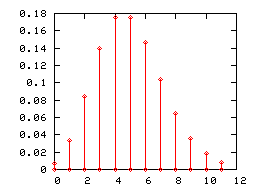
الرسوم البيانة ذات الأعمدة
ككل توزيع قائم على احتمال منفصل، يمكن تمثيل توزيع بواسون برسوم بيانية ذات أعمدة. هنا تحت، تمثل الرسوم البيانية توزيع بواسون ذا المعلمات 1 و 2 و 5.
رسم توزيع بواسون ذا العامل 5 بدأ يشبه بعض الشيء التوزيع الطبيعي (أو التوزيع الغاوسي) ذا القيمة المتوقعة 5 التباين 5. ولذلك إذا كانت λ أكبر من 5، نخير استعمال نموذج التوزيع الطبيعي.
بعض الخاصيات
إذا كانتا X و Y متغيران عشوائيان مستقلاّن يتبعان توزيع بواسون ،الأولى مع المعلمة λ والثانية المعلمة μ فإنّ X+Y متغير عشوائي يتبع توزيع بواسون ذا المعلمة λ+μ.
المراجع
- ↑ p963-965, Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 0-393-04002-X ISBN 978-0-393-04002-9
اقرأ أيضا
- توجد جداول للمساعدة على حساب احتمال بمعرفة λ و k. موقع الجدول في ويكي مصدر العربية: جدول توزيع بواسون
bg:Разпределение на Поасон ca:Distribució de Poisson cs:Poissonovo rozdělení de:Poisson-Verteilung el:Κατανομή Poisson en:Poisson distribution es:Distribución de Poisson eu:Poissonen banakuntza fa:توزیع پواسون fi:Poissonin jakauma fr:Loi de Poisson he:התפלגות פואסון hu:Poisson-eloszlás it:Distribuzione di Poisson ja:ポアソン分布 ko:푸아송 분포 lt:Puasono skirstinys nl:Poissonverdeling no:Poissonfordeling nov:Distributione de Poisson pl:Rozkład Poissona pt:Distribuição de Poisson ru:Распределение Пуассона simple:Poisson distribution sl:Poissonova porazdelitev su:Sebaran Poisson sv:Poissonfördelning tr:Poisson dağılımı uk:Розподіл Пуассона vi:Phân phối Poisson zh:泊松分佈 zh-yue:Poisson distribution









![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24650c837524f593a60e41f7371b39de75512d5c)