الفرق بين المراجعتين لصفحة: «قطع مخروطي»
ط (١ مراجعة: الصفحات في تصنيف رياضيات) |
(شكر) |
||
| سطر 1: | سطر 1: | ||
{{شكر|ويكيبيديا}} | |||
[[File:Conic sections with plane.svg|left|450px|thumb|أنواع القطوع المخروطية:<br /> 1. قطع مكافئ<br /> | [[File:Conic sections with plane.svg|left|450px|thumb|أنواع القطوع المخروطية:<br /> 1. قطع مكافئ<br /> | ||
2. دائرة وقطع ناقص<br /> | 2. دائرة وقطع ناقص<br /> | ||
| سطر 132: | سطر 134: | ||
[[تصنيف:رياضيات]] | [[تصنيف:رياضيات]] | ||
[[تصنيف:قطوع مخروطية]] | [[تصنيف:قطوع مخروطية]] | ||
المراجعة الحالية بتاريخ 05:16، 11 أكتوبر 2012
| هذا المقال تم نقل معظمه من موقع |
| ويكيبيديا |
في الهندسة الوصفية القطعة المخروطية هو منحنى يُحصل عليها عند تقاطع مخروط بسطح لا يمر برأس وغير مماس له (التقاطع في هذه الحالات نقطة أو مستقيم).
دُرست القطع المخروطية منذ وقت طويل يعود إلى 200 قبل الميلاد عندما قام أبولونيو (apollonius من perga) بإجراء دراسة تبين خصائصها.
التعريف التحليلي
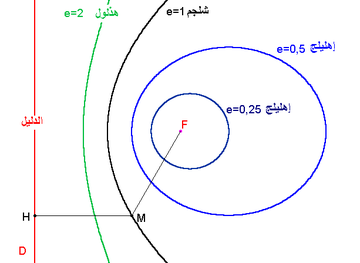
في التحليل الرياضي القطوع المخروطية، هو المحل الهندسي لنقطة تتحرك بحيث تكون النسبة بين بعدها عن نقطة ثابتة وبعدها عن مستقيم ثابت تساوي نسبة ثابتة. تسمى هذه النسبة الإختلاف المركزي (Eccentricity)، كما تسمى النقطة الثابتة البؤرة (Focus)، أما المستقيم الثابت فيدعى الدليل (directrix).
حيث:
- P هي نقطة (x,y) تقع على القطع
- S البؤرة
- e معامل الاختلاف المركزي
- و m هي مسقط العمودي ل P على الدليل
إذا كان الإختلاف المركزي مساويا للوحدة (عدد الواحد الصحيح) سمي المنحنى قطعا مكافئا (Parabola)، وإذا كان الإختلاف المركزي أقل من الوحدة (الواحد الصحيح) سمي المنحنى قطعا ناقصا (Ellipse)، وإذا كان الإختلاف المركزي أكبر من الوحدة(الواحد) سمي المنحنى قطعا زائدا(Hyperbola).
وتسمى القطوع المكافئة والناقصة والزائدة بالقطوع المخروطية، لأنه يمكن أن تتولد نتيجة قطع السطح المخروطي بمستو في وضع معين.
أنواع القطوع المخروطية
لها ثلاثة أنواع هي القطع المكافئ(شلجم)، الزائد(هذلول)،والناقص(اهليج). وقد تعتبر الدائرة نوعاً رابعاً (كما اعتبرها أبولونيو)أو يمكن اعتبارها نوع من القطوع الناقصة. يتشكل القطع الناقص والدائرة عندما يكون تقاطع المستوى والمخروط منحنى مغلق. تتشكل الدائرة عندما يكون المستوى القاطع موازيً لدائرة القاعدة المولدة للمخروط- بالنسبة لمخروط يميني (كما في الشكل المقابل في أعلى الصورة) يكون المستوى القاطع عمودياً على محور تماثل المخروط.إذا كان المستوى القاطع موازي لخط واحد فقط من الخطوط المولدة للمخروط حينها يصبح القطع مفتوحاً وليس مغلقاً فيسمى قطعاً مكافئاً. وفي الحالة الأخيرة يتكون القطع الزائد عندما يتقاطع المستوى مع نصفي المخروط الإثنين، مكوناً بذلك منحنيين منفصلين ومفتوحين، يتم في الغالب تجاهل أحدهما والعمل بالآخر.
حالات شاذة
يوجد عدد من الحالات الشاذة تحدث عندما يمر المستوى القاطع برأس المخروط Apex. التقاطع في هذه الحالات قد يكون خطاً مستقيما ً(إذا كان المستوى مماساً لسطح المخروط)؛ أو نقطة(إذا كان الزاوية بين المستوى ومحور المخروط أكبر من المماس)؛ أو زوج من الخطوط المتقاطعة (عندما تكون الزاوية أصغر).
عندما يصبح المخروط أسطوانة -عندما يكون الرأس واقع في منطقة اللانهاية نتحصل على قطوع أسطوانية. بالرغم من أن ذلك يتسبب غالباً في قطع ناقص أو دائرة، إلا ان هناك حالة شاذة تنتج خطين متوازيين.
الإختلاف المركزي
- انظر أيضاً: لا مركزية (رياضيات)
شروط التعريف الأربعة الواردة أعلاه يمكن جمعها في شرط واحد يعتمد على نقطة افتراضية F(البؤرة) ومستقيم L (الدليل)لا يمر بـ Fوعدد حقيقي غير سالب e (معامل الإختلاف المركزي).القطع المخروطي المقابل يتكون من جميع النقاط التي تبعد عن F مسافةً تساوي e مرة بعدها عن L. إذا كانت e بين 0 و 1 نحصل على قطع ناقص، إذا كانت e=1 نتحصل على قطع مكافئ وإذا كانت أكبر من 1 نحصل على قطع زائد.
هناك دليلين وبؤرتين لكل من القطع الزائد والناقص. المسافة من المركز إلى الدليل هي ، بينما هو المحور شبه الأكبر- semi-major axis - للقطع الناقص، أو المسافة من المركز إلى قمة القطع الزائد. المسافة من المركز للبؤرة هي .
في حالة الدائرة يكون معامل الإختلاف المركزي e= 0 ويمكن تخيل أن الدليل قد تم استبعاده لانهائياً عن المركز. لكن من غير المفيد استخدام التعبير: ان الدائرة تتكون من كل النقاط التي التي تبعد مسافة e مرة بعدها عن L لأننا سنحصل على 0 ضرب مالانهاية!
لذلك فإن الإختلاف المركزي للقطع المخروطي هو مقياس يبين لأي مدى يبعد القطع عن أن يكون دائرة. لقيمة معطاة ، كلما اقتربت من 1 كلما نقص طول المحور شبه الأصغر semi-minor axis.
المعادلة الجبرية
يمكن إعطاء معادلة القطع المخروطي بأشكال مختلفة منها:
- إذا كان الأختلاف المركزي يساوي هـ وكانت البؤرة عند نقطة الأصل (.،.) والدليل مستقيما عموديا على محور السينات يقطعه على بعد ف فإن معادلة القطع المخروطي تعطى بالمعادلة التالية:
(1 - هـ2)س2 + 2هـ2 ف س + ص2 = هـ2 ف
- معادلة من الدرجة الثانية في متغيرين س، ص ويمكن كتابة هذه المعادلة على الصورة التالية:
أ س2 + 2ب س ص + جـ ص2 +2د س +2هـ ص + و=.
الإحداثيات الديكارتية
في النظام الإحداثي الديكارتي، المنحنى لدالة تربيعية في متغيرين هو دائماً قطع مخروطي، وكل القطوع المخروطية تتكون بهذه الطريقة. معادلتها تكون في الصورة:
- حيث , , ليسوا جميعاً أصفاراً.
إذن:
- إذا كانت ، نحصل على معادلة قطع ناقص(مالم يكن المخروط منحل، مثلاً )؛
- إذا كان و المعادلة تمثل دائرة؛
- إذا كان ، نحصل على معادلة قطع مكافئ.
- إذا كان ، نحصل على معادلة قطع زائد.
- أيضاًإذا كان ،نحصل على معادلة قطع زائد مستطيل.
لاحظ أن A و B هناهي مجرد معاملات ولا تمثل أي أطوال للمحاور الأكبر والأصغر كما سيتم تعريفها في القسم التالي
في تعبير المصفوفات تصبح المعادلات السابقة كالتالي:
أو
و
- .
رغم تغيير الإحداثيات يمكن وضع هذه المعادلات في صورة قياسية:
- الدائرة:
- القطع الناقص:
- القطع المكافئ:,
- القطع الزائد:
- القطع الزائد المستطيل:
مثل هذه الصيغ تكون متماثلة حول محور x، وبالنسبة للدائرة، القطع الزائد، والناقص حول محور y القطع الزائد المستطيل هي حالة التماثل الوحيدة التي تكون حول و. لذلك فان دالتها العكسية هي نفس الدالة الأصلية.
يمكن كتابة هذه الصيغ القياسية في صورة معادلات وسيطية (بارامترية):
- الدائرة:
- القطع الناقص:
- القطع المكافئ:
- القطع الزائد: أو
- القطع الزائد المستطيل:
الإحداثيات المتجانسة
في الإحداثيات المتجانسة، القطع المخروطي يمكن تمثيله بـ:
أو في تعبير المصفوفات:
المصفوفة تدعى "مصفوفة القطع المخروطي". تدعى محددة القطع المخروطي. إذا كان Δ = 0 فإن القطع المخروطي يسمى "منحلاً Degenerate"، وهذا يعني أنه في الحقيقة عبارة عن اتحاد خطين مستقيمين. أي قطع مخروطي يتقاطع مع نفسه هو قطع منحلة ،ولكن ليس كل القطوع المنحلة تقاطع نفسها ،وفي هذه الحالة يكون القطع خطاً مستقيماً.
على سبيل المثال القطع المخروطي يختزل اتحاد المستقيمين:
.
وبالمثل يختزل القطع المخروطي أحياناً خطاً مفردا:
.
يدعى مميز القطع المخروطي. إذا كان δ = 0 فالقطع المخروطي مكافئ، إذا كان δ<0 فهو زائد، واذا كان δ>0 فهو ناقص. إذا كان δ>0 و A1 = A2 فهي دائرة، أما إذا كان δ<0 و A1 = -A2 فهو قطع زائد مستطيل. يمكن اثبات أنه في مستوى الإسقاط المركب CP2 قطعين مخروطيين بـ 4 نقاط مشتركة(إذا أخذنا في الاعتبار التعددية Multiplicity)أي لا يوجد اكثر من 4 نقاط تقاطع ويوجد دائماً نقطة تقاطع واحدة(الإحتمالات: 4 نقاط تقاطع مختلفة، نقطتي تقاطع فرديتين ونقطة تقاطع مزدوج، نقطتي تقاطع مزدوج، نقطة تقاطع فردي ونقطة تقاطع بتعددية 3، نقطة تقاطع واحدة بتعددية 4). إذا وجدت نقطة تقاطع واحدة على الأقل ذات تعددية>1، يقال بأن القطعين المخروطيين متماسين. إذا كان هناك نقطة تقاطع واحدة ذات تعددية 4 يقال ان القطعين متلامسين osculating.
إضافة لذلك، كل خط مستقيم يقاطع كل من القطعين المخروطيين مرتين. إذا كانت نقطة التقاطع مزدوجة يعتبر الخط مماساً ويسمى المماس. لأن كل مستقيم يقاطع القطع مرتين فإن كلا القطعين المخروطيين له نقطتين في المالانهاية(تقاطع النقاط مع خط المالانهاية) إذا إذا كانت النقطتين حقيقيتين فلابد أن يكون القطع زائداً، واذا كانتا تخيليتين فلابد أن يكون القطع ناقصاً، اما إذا كان للقطع نقطة واحدة مزدوجة في مالانهاية فهو مكافئ.
مواضيع ذات صلة
مصادر
- معجم الرياضيات - تأليف لجنة من الخبراء من وزارة التربية والتعليم - عمان - طبعة مكتبة لبنان - ساحة رياض الصلح/ بيروت - 1980م.