مصفوفة

يشار عادة إلى عناصر المصفوفة بحرف صغير أسفله رقمين الأول يشير إلى رقم السطر والثاني إلى رقم العمود.

يعتبر حساب المصفوفات من الأدوات الرياضية الهامة لدراسة مواضيع مختلفة مثل الكهرباء والكيمياء والإحصاء والبرمجيات إضافة إلى الرياضيات البحتة.

تعرف المصفوفة في الرياضيات بأنها مجموعة مستطيلة من الأرقام منتظمة بشكل أعمدة وأسطر

${\begin{bmatrix}1&9&13\\20&55&4\end{bmatrix}}$

يدعى كل جزء رقم في المصفوفة بعنصر أو مدخل. كمثال على المدخلات في المصفوفة أعلاه 1, 9, 13, 20, 55 ,4. يدل عادة على أي مدخل في مصفوفة ما باسم المصفوفة بحرف لاتيني صغير وأسفله رقمين صغيرين بحيث يمثل الرقم الأول رقم الصف والثاني رقم العمود مثل الشكل المرفق. يمكن جمع وطرح المصفوفات ذات نفس القياس. كما يمكن ضرب المصفوفات بأنسجام معين في القياس. ولهذه العمليات العديد من خصائص الحساب العادي, باستثناء أن ضرب المصفوفات ليس بعملية تبديلية, وبشكل عام يمكن أن نقول أن A.B لا يساوي B.A. تعرف المصفوف المؤلفة من صف واحد أو عمود واحد بمتجه. أما المصفوفة ذات القياس الأكبر تعرف بموتر.

تعتبر المصفوفات من إحدى أهم مفاتيح الجبر الخطي. فيمكن أن تستخدم المصفوفات في حل النقل الخطي. يتوافق ضرب المصفوفات مع النقل الخطي الدالة المركبة. كما يمكن للمصفوفات تتبع المعاملات في نظام المعادلات الخطية

يمكن تعريف المصفوفة عامة على أنها دالة رياضية خطية تحول مجموعة بداية أي انطلاق (مجال) إلى مجموعة وصول أو نهاية (مدى). مجموعة الانطلاق والوصول يمكن أن تكون متكونة من أعداد صحيحة أو عقدية أو أشعة من الأعداد كما يمكن أن تكون هاتان المجموعتان متكونة بدورها من دالات رياضية أو أشعة دالات رياضية. ويمكن أن نرمز للمصفوفة بمعقفين يكتب بينهما عناصر المصفوفة كما هو مبين أسفله:
${\begin{bmatrix}{a}_{11}&{a}_{12}&\cdots &{a}_{1n}\\{a}_{21}&{a}_{22}&\cdots &{a}_{2n}\\\vdots &\ddots &\ddots &\vdots \\{a}_{m1}&{a}_{m2}&\cdots &{a}_{mn}\end{bmatrix}}$
حيث ${a}_{ij}$ يمكن أن تكون أعدادا صحيحة أو مركبة كما يمكن أن تكون دالات رياضية. ==

المصفوفة كتابع

إن مصفوفة من الشكل $\,m\times n\,\,(m,n\in \mathbb {N} )$، هي عبارة عن تابع: $\mathbf {A} \colon \{1,2,\ldots ,m\}\times \{1,2,\ldots ,n\}\to \mathbf {S} ,\,\,$

إن $(\{1,2,\ldots ,m\}\times \{1,2,\ldots ,n\}\,$ هو الجداء الديكارتي لكل من$\{1,2,\ldots ,m\}\,$ و$\{1,2,\ldots ,n\}.)\,$.

التعريف

تعرف المصفوفة هي تنظيم مستطيل الشكل لمجموعة من الاعداد على هيئة صفوف واعمدة محصورة بين قوسين. على سبيل المثال:

$\mathbf {A} ={\begin{bmatrix}9&8&6\\1&2&7\\4&9&2\\6&0&5\end{bmatrix}}$

يمكن أن تضع المصفوفة بين قوسين مربعين أو بين قوسين هلالليين

$\mathbf {A} ={\begin{pmatrix}9&8&6\\1&2&7\\4&9&2\\6&0&5\end{pmatrix}}$

تدعى الخطوط الأفقية في المصفوفة بالأسطر بينما تدعى الخطوط العمودية باسم عمود. أما الأرقام فتدعى مدخلات المصفوفة أو عناصر المصفوفة. ترمز أي مصفوفة بحرف لاتيني كبير وتحته رقمين على شكل جداء هما m,n بحيث يرمز m لعدد الصفوف و n عدد الأعمدة وبالتالي تعرف المصفوفة بعدد الصفوف والأعمدة (m × n مصفوفة), وتعرف m و n بأبعاد المصفوفة. فأبعاد المصفوفة أعلاه هي 4*3 أي 4 أسطر و 3 أعمدة

أما المصفوفة ذات العمود الواحد تحدد بالشكل (m × 1 مصفوفة) وتعرف باسم متجه عمودي. بينما المصفوفة المؤلفة من صف وحيد و n عمود تحدد بالشكل (a 1 × n مصفوفة) وتعرف باسم متجه صفي .

العمليات على المصفوفات

الجمع

لكى يتسنى جمع مصفوفتين فلابد ان يكونا من نفس القياس. ويعرف حاصل جمع مصفوفتين بأنه المصفوفة الناتجة من جمع العناصر المتناظرة في المصفوفتين. فيتم جمع العناصر الناتجة من تقاطع نفس الأعمدة والأسطر في كلا المصفوفتين وفق القاعدة:
${\begin{bmatrix}{a}_{11}&{a}_{12}&\cdots &{a}_{1n}\\{a}_{21}&{a}_{22}&\cdots &{a}_{2n}\\\vdots &\ddots &\ddots &\vdots \\{a}_{m1}&{a}_{m2}&\cdots &{a}_{mn}\end{bmatrix}}$ + ${\begin{bmatrix}{b}_{11}&{b}_{12}&\cdots &{b}_{1n}\\{b}_{21}&{b}_{22}&\cdots &{b}_{2n}\\\vdots &\ddots &\ddots &\vdots \\{b}_{m1}&{b}_{m2}&\cdots &{b}_{mn}\end{bmatrix}}$= ${\begin{bmatrix}{a}_{11}+{b}_{11}&{a}_{12}+{b}_{12}&\cdots &{a}_{1n}+{b}{1n}\\{a}_{21}+{b}_{21}&{a}_{22}+{b}_{22}&\cdots &{a}_{2n}+{b}_{2n}\\\vdots &\ddots &\ddots &\vdots \\{a}_{m1}+{b}_{m1}&{a}_{m2}+{b}_{m2}&\cdots &{a}_{mn}+{b}_{mn}\end{bmatrix}}$
.

فعلى سبيل المثال إذا كان

ِ$A={\begin{bmatrix}1&2&3\\0&-1&2\end{bmatrix}}$ ,$B={\begin{bmatrix}0&-1&2\\7&2&3\end{bmatrix}}$

فإن $C=A+B={\begin{bmatrix}1&1&5\\7&1&5\end{bmatrix}}$

ضرب مصفوفة وحيدة العنصر مع مصفوفة متعددة العناصر

نضرب العنصر الوحيد مع كل عنصر من عناصر المصفوفة، وتكون النتيجة، مصفوفة جديدة، تحوي العدد نفسه من العناصر. ${\begin{bmatrix}5&3&2\\1&7&6\end{bmatrix}}*2={\begin{bmatrix}10&6&4\\2&14&12\end{bmatrix}}$

ضرب مصفوفة في مصفوفة

رسم تخطيطي يوضح طريقة ضرب مصفوفة A بمصفوفة B.

• يجب في البداية أن نعلم أن ضرب المصفوفات غير تبديلي.
• من أجل إيجاد ناتج ضرب مصفوفتين (وهو مصفوفة)، يجب أن يتحقق الشرط التالي:

عدد الأعمدة في المصفوفة الأولى = عدد الأسطر في مصفوفة الثانية.

بفرض A مصفوفة من الشكل a x b، وB مصفوفة من الشكل c x d، فمن أجل إيجاد $A*B$، يجب أن يكون b=c.

سنبدأ في البداية بضرب مصفوفة وحيدة السطر مع مصفوفة وحيدة العمود، فبفرض A وB مصفوفتان، حيث:

$A={\begin{bmatrix}a_{1}&a_{2}&a_{3}\end{bmatrix}}$

$B={\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}$

فيكون: $A*B={\begin{bmatrix}(a_{1})(b_{1})+(a_{2})(b_{2})+(a_{3})(b_{3})\end{bmatrix}}$

ونلاحظ أن المصفوفة الناتجة هي مصفوفة وحيدة العنصر، وبالتالي، فإن ضرب مصفوفة وحيدة السطر مع مصفوفة وحيدة العمود ينتج مصفوفة وحيدة العنصر.

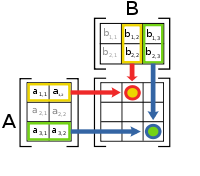
أما عند ضرب مصفوفتين متعددتي العناصر (وبفرض تحقق شروط الضرب)، فعندئذ، نقوم بتقسيم المصفوفة الأولى إلى سطور، والثانية إلى أعمدة، ونقوم بضرب الصف الأول بالعمود الأول (والنتيجة هي العنصر a_11 من النتيجة)، ثم نقوم بضرب الصف الأول مرة أخرى بالعمود الثاني (والنتيجة هي العنصر a_12 من النتيجة، وهكذا.

أمثلة على الضرب

مثال توضيحي بالرموز:

بفرض: $A={\begin{bmatrix}{a}_{11}&{a}_{12}&{a}_{13}\\{a}_{21}&{a}_{22}&{a}_{23}\end{bmatrix}}$

$B={\begin{bmatrix}{b}_{11}&{b}_{12}\\{b}_{21}&{b}_{22}\\{b}_{31}&{b}_{32}\end{bmatrix}}$

فيكون:

$A*B={\begin{bmatrix}({a}_{11}\times {b}_{11}+{a}_{12}\times {b}_{21}+{a}_{13}\times {b}_{31})&({a}_{11}\times {b}_{12}+{a}_{12}\times {b}_{22}+{a}_{13}\times {b}_{32})\\({a}_{21}\times {b}_{11}+{a}_{22}\times {b}_{21}+{a}_{23}\times {b}_{31})&({a}_{21}\times {b}_{12}+{a}_{22}\times {b}_{22}+{a}_{23}\times {b}_{32})\end{bmatrix}}$

مثال بالأرقام:

${\begin{bmatrix}1&0&2\\-1&3&1\\\end{bmatrix}}\times {\begin{bmatrix}3&1\\2&1\\1&0\\\end{bmatrix}}={\begin{bmatrix}(1\times 3+0\times 2+2\times 1)&(1\times 1+0\times 1+2\times 0)\\(-1\times 3+3\times 2+1\times 1)&(-1\times 1+3\times 1+1\times 0)\\\end{bmatrix}}$

$={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}.$

منقول مصفوفة

يعرف منقول المصفوفة بأنه المصفوفة الناتجة عن المصفوفة A_mxn بعد أن يتم تبديل الأعمدة بالأسطر وبالتالي تصبح A_nxm ويرمز لها بالرمز A^T. يلاحظ أن العنصر الذي يقع في الصف i والعمود j في المصفوفة A، سيقع في الصف j والعمود i في منقول المصفوفة. .

كمثال على منقول المصفوفة: المصفوفة A = ::${\begin{bmatrix}1&9&13\\20&55&4\end{bmatrix}}$ يصبح مقلوبها ::${\begin{bmatrix}1&20\\9&55\\13&44\\\end{bmatrix}}$

من خواص منقول المصفوفة:

• منقول مجموع مصفوفتين هو مجموع منقول هاتين المصفوفتين أي أن :

A+B)^T = A^T + B^T)

• إن منقول حاصل ضرب مصفوفتين يساوي حاصل ضرب المصفوفتين بشكل معاكس لمنقولهما أي:

A.B)^T = B^T × A^T)

معكوس المصفوفة

معكوس المصفوفة يقصد به المعكوس الضربى للمصفوفة بحيث يكون حاصل ضرب المصفوفة في معكوسها يساوى مصفوفة الوحدة.

تدعى المصفوفة A مصفوفة قابلة للعكس إذا وجدت مصفوفة B تحقق العلاقة التالية:

AB = I_n

و تدعى المصفوفة B بمقلوب المصفوفة A ويرمز لها بالرمز A⁻¹. يكون للمصفوفة المربعة من الدرجة n إذا كانت مصفوفة غير شاذة ويكون معكوسها وحيد. ويحسب معكوس المصفوفة من العلاقة :

$\mathbf {A} ^{-1}={1 \over {\begin{vmatrix}\mathbf {A} \end{vmatrix}}}\left(\mathbf {C} ^{\mathrm {T} }\right)_{ij}={1 \over {\begin{vmatrix}\mathbf {A} \end{vmatrix}}}\left(\mathbf {C} _{ji}\right)={1 \over {\begin{vmatrix}\mathbf {A} \end{vmatrix}}}{\begin{pmatrix}\mathbf {C} _{11}&\mathbf {C} _{21}&\cdots &\mathbf {C} _{n1}\\\mathbf {C} _{12}&\mathbf {C} _{22}&\cdots &\mathbf {C} _{n2}\\\vdots &\vdots &\ddots &\vdots \\\mathbf {C} _{1n}&\mathbf {C} _{2n}&\cdots &\mathbf {C} _{nn}\\\end{pmatrix}}$

حيث |A| محدد المصفوفة A وC_ij المصفوفة المرافقة:

و يكون بالتالي معكوس المصفوفة المربع ذات الدرجة الثاني :

$\mathbf {A} ^{-1}={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}^{-1}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.$

تتمتاز معكوس المصفوفة بالخصائص التالية:

• معكوكس معكوس مصفوفة هو المصفوفة الأصلية نفسها أي:

$\left(\mathbf {A} ^{-1}\right)^{-1}=\mathbf {A}$.

• منقول معكوس مصفوفة يساوي إلى معكوس منقول المصفوفة أي:

$(\mathbf {A} ^{\mathrm {T} })^{-1}=(\mathbf {A} ^{-1})^{\mathrm {T} }\,$

• معكوس جداء مصفوفتين يساوي إلى حاصل ضرب معكوس المصفوفة الثانية في معكوس المصفوفة الأولى أي:

$\left(\mathbf {AB} \right)^{-1}=\mathbf {B} ^{-1}\mathbf {A} ^{-1}$

مثال على تحويل من مجموعة انطلاق إلى مجموعة وصول

لنعتبر مثلا الشعاع التالي:
$V={\begin{bmatrix}{s}_{1}\\{s}_{2}\\{s}_{3}\\{s}_{4}\end{bmatrix}}\in {R}^{4}$
و المصفوفة التالية: $A={\begin{bmatrix}{a}_{11}&{a}_{12}&{a}_{13}&{a}_{14}\\{a}_{21}&{a}_{22}&{a}_{23}&{a}_{24}\end{bmatrix}}$

عملية تحويل الشعاع تتم على نحو النحو التالي:
$X=A*V={\begin{bmatrix}{a}_{11}&{a}_{12}&{a}_{13}&{a}_{14}\\{a}_{21}&{a}_{22}&{a}_{23}&{a}_{24}\end{bmatrix}}{\begin{bmatrix}{s}_{1}\\{s}_{2}\\{s}_{3}\\{s}_{4}\end{bmatrix}}={\begin{bmatrix}{a}_{11}{s}_{1}+{a}_{12}{s}_{2}+{a}_{13}{s}_{3}+{a}_{14}{a}_{14}\\{a}_{21}{s}_{1}+{a}_{22}{s}_{2}+{a}_{23}{s}_{3}+{a}_{24}{s}_{4}\end{bmatrix}}$

وهكذا نكون قد حولنا شعاعا V ينتمي إلى ${R}^{4}$ إلى شعاع X ينتمي إلى ال ${R}^{2}$. أما عامة إذا كانت المصفوفة تحتوي على عدد m من الأسطر و n من الأعمدة فإنها تحول مجموعة الانطلاق المكونة من أشعة تنتمي إلى ال ${K}^{n}$ إلى مجموعة الوصول المتكونة من أشعة تنتمي إلى ال ${K}^{m}$.
كما يمكن اعتبار المصفوفات نوعا خاصا من التنسورات ألا وهي التنسورات من الدرجة الثانية

حساب المحدد

حساب قيمة محدد الدرجة الثالثة: هناك طريقتان لحساب محدد مصفوفة من الدرجة الثالثة

الطريقة الأولى: 1. نكرر كتابة العمود الأول والثاني على الترتيب بعد العمود الثالث. 2. نكون مجموع حاصل ضرب العناصر الواقعة على الخطوط المستقيمة المتجهة من اليسار إلى اليمين ونطرح منه مجموع حاصل ضرب العناصر الواقعة على الخطوط المستقيمة المتجهة من اليمين إلى اليسار.

توضيح

a11 a12 a13 a11 a12

              a 21 a22  a23  a21  a22       

                  a31  a32  a33  a31  a32

الطريقة الثانية:

ملحوظة: الطريقة الأولى لا تصلح للتطبيق على محددات المصفوفات حيث بينما الطريقة الثانية يمكن تعميمها على محدد أي مصفوفة مع الاستفادة من خواص المحددات السابقة للتقليل من العمليات الحسابية.

الفك عن طريق المتعاملات: إذا كانت مصفوفة من الدرجة نفرض أن هي المصفوفة الناتجة من المصفوفة A بعد حذف الصف رقمi والعمود رقم j في لمصفوفة A المحدد تسمى المحددة الصغرى للعنصر ويعرف متعامل العنصر بأنه

ولأي مصفوفة مربعة يتحقق الآتي مجموع حاصل ضرب عناصر أي صف أو عمود في متعاملاتها يعطي قيمة المحدد أي انه إذا كانت مصفوفة من الدرجة فان 1. ويسمى مفكوك المحدد حول الصف رقم i

2. 3. ويسمى مفكوك الصف حول العمود

بالنسبة للمصفوفات التي تكون من الدرجة الرابعة أو أكثر يستحسن تحويلها إلى مصفوفة مثلثية لتبسيط حساب المحدد وبالتالي يصبح يساوي جداء عناصر القطر الرئيسي للمصفوفة المثلثية الجديدة

حساب القيمة المطلقة لمصفوفة

يتم حساب القيمة المطلقة للمحدده اعتمادا على قيمه المحدد

المعادلات الخطية

إذا وضع عدد من المتغيرات x في متجه عمودي حيث n عدد المتغيرات وبذلك يتكون المتجه من المتغيرات x₂,..., x_n, و A مصفوفة ذات قياس nxm بحيث تتألف مدخلات المصفوفة من ثوابت المتغيرات, و b متجه عمودي يتألف من ثوابت المعادلات فإن:

Ax = b

بحيث:

a_1,1x₁ + a_1,2x₂ +... + a_1,nx_n = b₁

و

a_m,1x₁ + a_m,2x₂ +... + a_m,nx_n = b_m.

المصفوفة المربعة

تعرف المصفوفة المربعة بأنها مصفوفة تحوي نفس العدد من الأسطر والأعمدة. فالمصفوفة nxn تعرف بمصفوفة مربعة ذات بعد n. يمكن جمع أو ضرب أي مصفوفتين مربعتين لهما نفس البعد. وتدعى المصفوفة A مصفوفة قابلة للعكس إذا وجدت مصفوفة B تحقق العلاقة التالية:

AB = I_n

و تدعى المصفوفة B بمقلوب المصفوفة A ويرمز لها بالرمز A⁻¹. كما يدعى مجموع عناصر القطر الرئيسي للمصفوفة بأثر المصفوفة (tr(A وبما أن الأثر التاتج من مصفوفتين مستقل فإن ضرب اثري مصفوفتين هو عملية تبديلية أي :

(tr(AB) = tr(BA. كما أن أثر مصفوفة يساوي أثر منقول المصفوفة 

tr(A) = tr(A)^T

لمحة تاريخية

للمصفوفات تاريخ طويل في استخدامها في حل المعادلات الخطية. فأقدم شكل لاستخدام المصفوفات في حل المعادلات كان نص صيني يدعى الفصول التسع في الرياضيات, كما تضمن مبدأ المحددات والذي يرجع تاريخه إلى ما بين 300 قبل الميلاد إلى 200 ميلادي , في سنة 1683 نشر بحث عن المصفوفات من قبل الرياضي الياباني سيكي تاكازاو. بعد ذلك نشر بحوث متعلقة بالمصفوفات العالم الألماني جوتفريد لايبنتز في سنة 1963. ومن ثم نشر جابرييل كرامر قواعده في الحساب سنة 1750.

ركزت نظريات المصفوفات المبكرة على دور المحددات بدلا عن المصفوفات بشكل مستقل. ولم يظهر مفهوم المصفوفة بشكل مستقل حتى وقت حديث, في سنة 1858 مع أرثر كايلي ونظرياته حول المصفوفات.